Sensibilidade, especificidade e curvas ROC: Um guia visual para não se confundir mais!
Um guia visual e intuitivo para descomplicar métricas de classificação

Descomplicando as métricas de classificação
Você já se viu diante do desafio de memorizar todas aquelas métricas de classificação?
“Era sensibilidade que priorizava acertar os positivos ou era especificidade? E a precisão… se refere a quê mesmo?"
Se você já se fez essas perguntas, não está sozinho. Essas métricas são confusas porque muitas vezes são ensinadas apenas com fórmulas matemáticas, sem uma compreensão visual ou prática do que realmente significam.
Neste post, vamos transformar conceitos abstratos em intuições visuais. Ao invés de decorar fórmulas, você vai entender o que cada métrica realmente representa e quando deve ser aplicada. Esta postagem inclui simulações interativas, assim você poderá observar como cada métrica se comporta em tempo real.
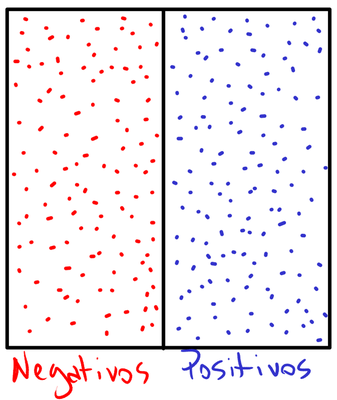
O cenário básico: separando positivos e negativos
No diagrama apresentado, utilizamos uma representação visual simplificada para facilitar a compreensão dos conceitos. O retângulo é dividido em duas seções distintas:
- Lado esquerdo: representa casos negativos (exemplos: pessoas sem doença, transação legítima, etc…);
- Lado direito: representa casos positivos (exemplos: pessoas com doença, transação fraudulenta, etc…).
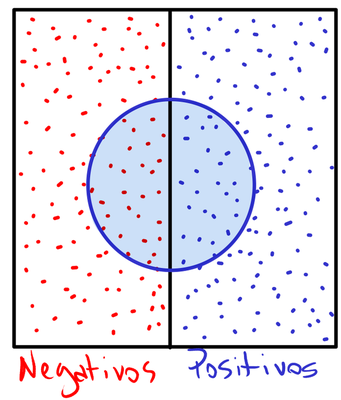
Para entender as métricas de classificação, podemos visualizar o que um modelo está fazendo. Considere que nosso modelo (por exemplo, que determina se a pessoa possui ou não determinada doença) é representado por um círculo azul no centro desse retângulo. O círculo, na verdade, é a fronteira de decisão do modelo. Tudo o que está dentro deste círculo o modelo prevê que é positivo. Portanto, tudo que está fora dele é previsto como negativo.
Observamos claramente que o modelo não é perfeito1. Ele comete dois tipos de erros:
- Classifica alguns negativos como positivos (dentro do círculo, à esquerda);
- Classifica alguns positivos como negativos (fora do círculo, à direita).
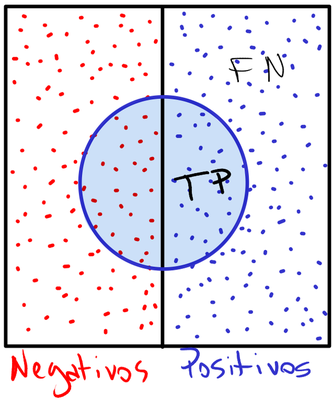
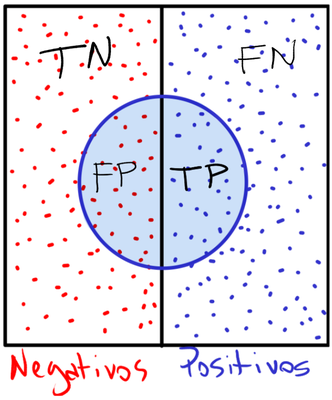
As quatro situações fundamentais
Esses erros2 e acertos possuem nomes e são representados nas quatro regiões da figura ao lado. Suas descrições são as seguintes:
| Sigla | Descrição |
|---|---|
| TP | Verdadeiro positivo, acerto |
| FN | Falso negativo, erro de omissão, subestimação |
| FP | Falso positivo, falso alarme, superestimação |
| TN | Verdadeiro negativo, rejeição correta |
Com base nessas quatro situações, podemos calcular métricas que nos ajudam a avaliar o desempenho de um modelo.
Entendendo Cada Métrica Visualmente
1. Sensibilidade (Recall ou TPR)
Pergunta-chave: “De todos os casos realmente positivos, quantos o modelo classificou como positivos?"
A sensibilidade indica quanto do lado direito foi coberto pelo círculo — ou seja, a proporção entre a parte azul dentro do círculo (TP) e todo o lado direito (TP + FN). O foco da sensibilidade é não deixar passar casos positivos.
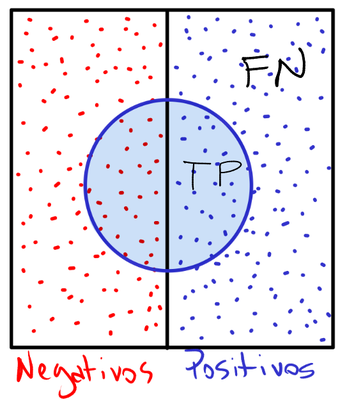
2. Taxa de Falsos Negativos (FNR)
Pergunta-chave: “De todos os casos realmente positivos, quantos o modelo classificou como negativos?"
É a proporção entre o que o círculo não cobriu do lado direito (FN) em relação ao lado direito inteiro (TP + FN).
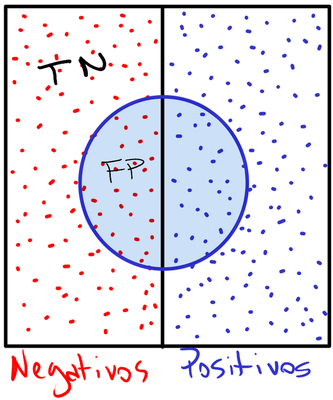
3. Especificidade (TNR)
Pergunta-chave: “De todos os casos realmente negativos, quantos o modelo classificou como negativos?"
A especificidade representa a proporção do lado esquerdo que o círculo não cobriu (TN) em relação ao lado esquerdo inteiro (TN + FP).
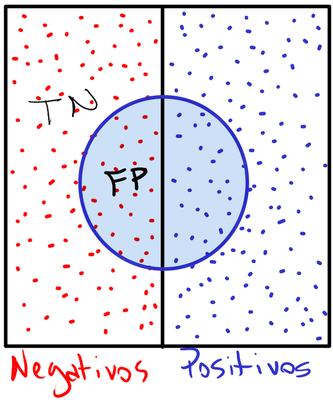
4. Taxa de Falsos Positivos (FPR)
Pergunta-chave: “De todos os casos realmente negativos, quantos o modelo classificou como positivos?"
É a proporção entre o que o círculo cobriu do lado esquerdo (FP) e o lado esquerdo inteiro (TN + FP). É o complemento da especificidade.
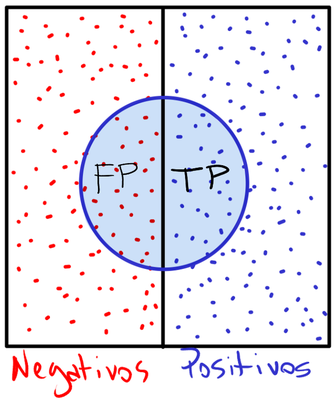
5. Precisão (Precision ou PPV)
Pergunta-chave: “Quando o modelo diz ‘positivo’, com que frequência ele está correto?"
Considerando a região interna do círculo (tudo o que o modelo classificou como positivo), a precisão representa a proporção da área à direita (TP) em relação à área total do círculo (TP + FP). O foco da precisão é não dar falsos alarmes.
6. Acurácia
Pergunta-chave: “Qual a porcentagem total de previsões corretas?"
A acurácia representa a proporção da área coberta pelo círculo à direita (TP) mais a área não coberta pelo círculo à esquerda (TN) em relação à área total.
Simulações interativas
Para realmente compreender esses conceitos, nada melhor que ver como eles se comportam em tempo real.
Métricas de classificação
A simulação abaixo ilustra interativamente os conceitos fundamentais de métricas de classificação. Pontos são uniformemente e aleatoriamente gerados, separados igualmente entre as classes positiva (direita) e negativa (esquerda). Você pode alterar o tamanho do cículo, bem como movê-lo e assim observar como se comportam as métricas discutidas acima.
Positives
Positives
Negatives
Negatives
Ao interagir com a simulação3, você poderá observar alguns casos interessantes:
- Precisão 50%: Ocorre quando o círculo está exatamente no centro.
- Baixo recall mas precisão de 100%: Um círculo pequeno está inteiramente no lado direito.
- Recall máximo com FPR máximo: O círculo cobre toda a área de simulação, e portanto o modelo classifica tudo como positivo. Obtemos apenas TP e FP; recall máximo, FPR máximo e nenhuma especificidade.
- Sem recall nem precisão: Se reduzirmos o tamanho do círculo a zero, o modelo classificará tudo como negativo, resultando em ausência de recall, precisão e FPR. Mesmo assim, temos uma acurácia de 50% e especificidade de 100%.
- O cenário ideal: Um grande círculo que tenta cobrir todo o lado direito e, ao mesmo tempo, possuir a menor área possível no lado esquerdo.
Essa visualização interativa é útil porque permite relacionar conceitos abstratos com representações visuais concretas. Por exemplo, quando alguém diz que “o modelo tem alta precisão, mas baixo recall”, você pode visualizar isso como um círculo pequeno, posicionado quase totalmente no lado direito. Já no caso de “alta especificidade, mas baixa sensibilidade”, uma possível representação seria um círculo centralizado, dividido igualmente entre os dois lados.
Entendendo a curva ROC
Modelos de classificação, como a regressão logística, geralmente não retornam apenas uma resposta binária (sim/não), mas sim uma probabilidade associada a cada classe. Ou seja, ao invés de dizer diretamente “positivo” ou “negativo”, o modelo indica quão confiante está de que determinada observação pertence à classe positiva — atribuindo um valor entre 0 e 1.
Para transformar essa probabilidade em uma decisão binária, é necessário definir um limiar (threshold). Por exemplo: se a probabilidade for maior que 0,5, classificamos como positivo; caso contrário, como negativo. Mas o que acontece se alterarmos esse valor de 0,5? Como o desempenho do modelo muda com diferentes limiares? É justamente aí que entra a curva ROC4. Em vez de avaliar o modelo com base em um único ponto de corte, a curva ROC mostra como o modelo equilibra acertos e erros à medida que o limiar varia. Para construí-la, plotamos TPR (eixo y) versus FPR (eixo x) para todos os limiares de 0 a 1.
O cenário baseline
Para entender melhor a curva ROC, vamos considerar a simulação anterior mas com um círculo estático que cresce exatamente do centro. Uma vez que os pontos estão uniformemente distribuidos no plano, para qualquer limiar, o modelo classifica corretamente os positivos (TPR) na mesma proporção que classifica incorretamente os negativos (FPR).
Quando plotamos a curva ROC para este modelo, obtemos uma reta diagonal do tipo $y = x$. Em outras palavras, se o modelo identifica 60% dos positivos corretamente, ele também classifica erroneamente 60% dos negativos como positivos. Varie o tamanho do círculo na simulação abaixo para observar esse comportamento.
Positives
Positives
Negatives
Negatives
Isso seria equivalente a um modelo que faz previsões aleatórias, como jogar uma moeda para decidir entre positivo e negativo. Ou seja, um modelo sem poder preditivo.
Um modelo melhor que o baseline
Um bom modelo de classificação consegue obter uma sensibilidade alta sem produzir muitos falsos positivos. Utilizando a mesma simulação, uma possibilidade seria um círculo que cresce com início inteiramente no lado direito (captando mais positivos inicialmente). Aumente o tamanho do círculo na visualização abaixo e observe o que acontece.
Positives
Positives
Negatives
Negatives
Como observamos, após certa medida, o círculo começa a captar parte do lado esquerdo, gerando falsos positivos. Quando plotamos a curva ROC nesse caso, obtemos uma curva que se arqueia para o canto superior esquerdo do gráfico5.
Vale a pena destacar que a curva ROC pode ser enganosa para conjuntos de dados muito desbalanceados. Como um último exemplo, vamos observar o que acontece com a curva nesse cenário.
Dados Desbalanceados
Quando os dados são altamente desbalanceados (por exemplo, fraude bancária onde menos de 0,1% das transações são fraudulentas), a curva ROC pode mascarar problemas de desempenho. Na curva ROC, os falsos positivos são medidos em relação ao número total de negativos (FPR = FP/N). Com muitos exemplos negativos, cada falso positivo tem um impacto pequeno na taxa de falsos positivos. Isso pode fazer com que um modelo pareça melhor do que realmente é. Para dados desbalanceados, considere usar a curva Precisão-Recall (PR).
A simulação abaixo mostra na prática a diferença entre as curvas ROC e PR. É possível alterar tanto o tamanho do círculo quanto a porcentagem da classe positiva no conjunto de dados. Varie primeiramente o tamanho do círculo e veja as duas curvas surgindo.
Positives
Positives
Negatives
Negatives
Repare que, com apenas 1% de exemplos positivos, aumentar o tamanho do círculo faz com que a curva PR sofra uma queda acentuada na precisão — já que o número de falsos positivos aumenta muito mais do que o de verdadeiros positivos. Esse efeito, porém, não é capturado pela curva ROC, que permanece praticamente inalterada.
Outro efeito interessante pode ser observado com a seguinte configuração: defina o tamanho do círculo em 40 e varie a porcentagem da classe positiva de 1% até 100%, e depois retorne a 1%. Você notará que o ponto correspondente na curva ROC praticamente não se move — a taxa de falsos positivos (FPR) permanece quase constante. Por outro lado, na curva PR, a precisão cai drasticamente à medida que a proporção de positivos se torna menor.
Em geral, com precisão e recall estamos mais focados na classe minoritária (positiva, nesse caso), o que torna essas métricas mais informativas para dados desbalanceados. Um falso positivo não tem muito peso na curva ROC se temos muitos exemplos negativos. Porém, o mesmo falso positivo terá um impacto maior na curva PR porque FP está no denominador da precisão.
-
Um modelo ideal seria representado por um retângulo idêntico ao lado direito, posicionado exatamente sobre ele. ↩︎
-
Os dois tipos de erros possuem nomes conhecidos. Falsos positivos (FP) são erros tipo I e falsos negativos (FN) são erros tipo II. ↩︎
-
Nas simulações desta postagem, os pontos estão distribuídos uniformemente no plano. Essa escolha tem fins didáticos, pois facilita a explicação dos conceitos. No entanto, vale lembrar que, na vida real, os dados não necessariamente seguem essa distribuição. ↩︎
-
A abordagem dessa postagem se aplica a casos binários (por exemplo, positivo/negativo). Para problemas multiclasse, teríamos uma curva ROC para cada classe (one-vs-all). ↩︎
-
Quanto mais próxima a curva ROC estiver do canto superior esquerdo, melhor é o desempenho do modelo. Para quantificar o desempenho, calculamos a área sob a curva (AUC), que representa a performance geral do modelo: AUC = 1,0: modelo perfeito. AUC = 0,5: modelo aleatório (sem poder preditivo). AUC < 0,5: pior que aleatório (inverta suas previsões). ↩︎